今年の京大の文系数学は易化したという話題で持ち切りのようです。
問1の2問も中学生でも解けるレベルの問題です。
問3(2)は正五角形を使った問題で三角関数を使えば難しくない問題ですが、
これを中学数学のみで解くとしたらどうやって解きますか?
そして、高校数学で解くなら簡単な問題ですが、この問題が出題された背景を考えてみます。
2023京大文系数学
— くま@浪人生 (@LeEV5gN4YmK7W6S) February 25, 2023
難易度はノーコメントで pic.twitter.com/o9nA4CGiaf
京大2023文系数学問3を中学数学で解いてみる
(1)cos2θとcos3θをcosθの式として表せ
これは教科書レベルの和積の公式を使えば解けますね。
これが(2)を三角関数を使って解くためのヒントにはなっています。
中学数学のみで(2)を解くならこの誘導問題は不要です。
(2)半径1の円に内接する正五角形の一辺の長さが1.15より大きいか否かを理由をつけて判定せよ

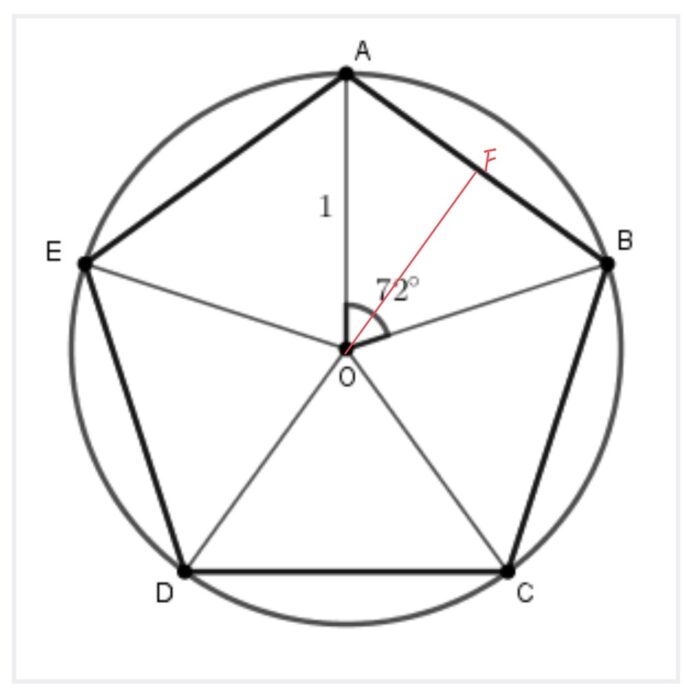
左の図をもとに考えてみます。
△OABを考えた時にABが1.15より大きいかどうかを考えればいいという問題です。
つまりAB/OAが1.15より大きいことが言えればいいのです。
OFは△OABが二等辺三角形なのでOから垂線を下した足をFとしてAF=BFが言えます。
AB/OA=2AF/OA=2AFの値と1.15の比較をすればいいのです。
ここで△AOFは36°、54°、90°の直角三角形です。
AFの長さを求めてみよう
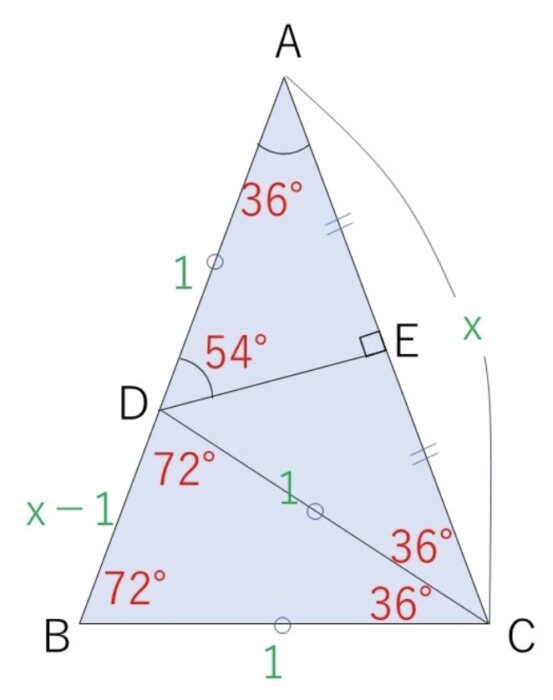
左図のような底辺BCの大きさが1で、内角が 36°,72°,72° の二等辺三角形を考えます。
∠C の2等分線を引いてABとの交点をDとする。
すると ∠CDB=72° だから△CBD は二等辺三角形。
また、∠ACD=36°より △DCA も二等辺三角形。
よって BC=CD=AD=1
ここで、△ABCと△CDB は相似だから
AC=AB=x とおくと x:1=1:x−1 ∴x=1+5–√2(x>0)
さらに DからACに垂線DEを下ろすと、△DCAは二等辺三角形だからAE=x/2
直角三角形ADE に着目します。
DE^2=AD^2-AE^2=(5-√5)/8、AD=1より
54°をはさむ辺の比の2乗は(5-√5)/8、かつDE^2も(5-√5)/8と言えます。
左の図からAB^2=2AF^2=4AF^2>(1.15)^2
∴(AF^2)=(5-√5)/8 >0.330625が言えるかを考える。
5.0176>5>4.9729より 2.24>√5>2.23
(5-2.23)/8 > (5-√5)/8 > (5-2.24)/8
∴0.34625 > (5-√5)/8 > 0.345 > 0.330625
したがって正五角形の一辺の長さが1.15より大きいことが言えた。
AF^2の値を求めるにあたりcos54°を求めているのですが、
おおもとになる考えは小学校で習う「比」です。
「比」という概念を、「三角関数」という概念に置き換えただけなのです。
この「比」という着眼点に着目出来たら「三角関数」を知らなくても解けるのです。
正五角形を作図してみよう!
以前、「コンパスって何のために使うもの?」ということでブログを書いています。
https://ameblo.jp/daigorobe/entry-12776566206.html
正五角形をコンパスを使って書くとしたらどうやって描いたららいいのかが以下のブログで説明されています。
https://math.nakaken88.com/textbook/master-construction-of-cyclic-regular-pentagon/
正五角形に隠された黄金比
「黄金比」って知ってますか?
1:(1+√5)/2で表される黄金比は人々が美しさを感じると言われています。
特に美感や安定感に優れているとされています。
特に西洋ではその傾向が強く、さまざまな建築や美術、商品のデザインなどに「黄金比」が取り入れられています。
https://business-textbooks.com/golden-ratio/
まとめ
この問題が出題された意図は何だと思いますか?
出題者でない限り本当の意図はわかりませんが、
半径1の円に内接する正五角形の一辺の長さの2乗が(5-√5)/2です。
2重根号をはずしても近似値しか出せないので、不等号の評価問題として出題したのでしょう。
でもその根底にあるのは、
普段よく見かける図形を描くにはどうしたらいいのかを考えるような勉強をしていますか?
ということを問いている気がします。
正三角形、正方形(正四角形)、正六角形はコンパスで簡単に描けるけど、
正五角形はどうすればいいんだろうか?
という問いです。

