以前紹介した【ブルーバックス】中学数学で解く大学入試問題 は中学生はもちろん、高校生も今一度自分が勉強している高校数学を見直す意味でもおすすめです。

メネラウスの定理
この本の中では、2-1の「高校数学と中学数学で解く」は
2024海城中の問題から | らふわく~Life&laugh work~算数・数学・趣味
この記事でとりあげている海城中の入試問題を使って、
①算数の解き方、②中学数学(メネラウスの定理)の解き方、③ベクトルの解き方
と3通りの解き方ができることを息子とおさらいしたことがあります。
斜交座標を使った考え方
息子からベクトルは今後、数3で勉強することになると聞きました。
私の時代は1年で数Ⅰ、2年で基礎解析と代数幾何、3年で微積と確率
という単元分けでベクトルは代数幾何で習いましたが、今の数学の科目の分け方がよくわかりません。
細かく科目を分ける意味がどこにあるのだろうか?
ところで、ベクトルのこの典型問題。
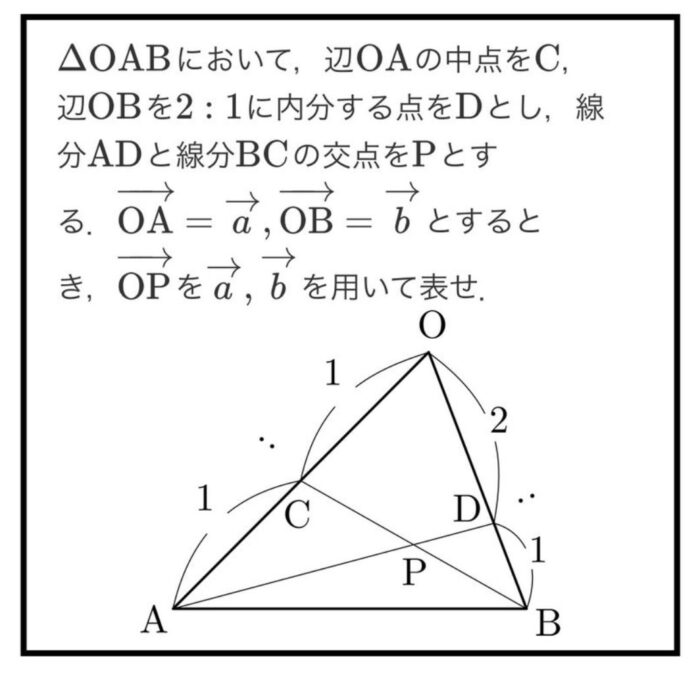
チェバの定理やメネラウスの定理を知っていれば、
1/1×3/1×DP/AP=1より AP:PD=3:1
よってOPベクトル=1/4OAベクトル+3/4×2/3OBベクトル
=1/4OAベクトル+1/2OBベクトルと瞬殺ですが
斜交座標という考え方を使うと別のアプローチができます。
たぶん学校では習わないかも。
ちなみに斜交座標に対して直交座標があります。
これはいわゆるX軸とY軸が直交したものであり、これは斜交座標の特別な場合です。
OAベクトル,OBベクトルを基底とする斜交座標を考えます。
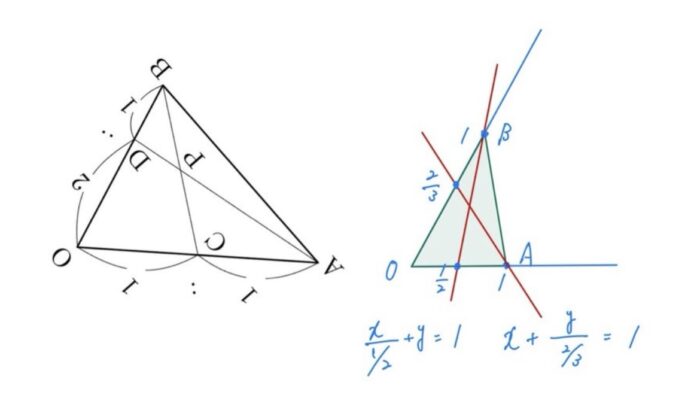
この斜交座標における直線ADの方程式は2x+3y=2,直線BCの方程式は2x+y=1
この2式を連立してx=1/4,y=1/2.したがって
OPベクトル=1/4OAベクトル+1/2OBベクトル
と考えることができます。
ベクトルと座標の融合ですね。
ベクトルの問題が中学1年生レベルの単純な連立方程式の問題に帰着します。
なお、直線はy=ax+bだけじゃなくx/a+y/b=1(切片型)と書けることもここで押さえておきましょう。
さいごに
この斜交座標の考え方を武器にしておくと、ベクトルの軌跡の問題も解けるようになります。
これが本当の先取り学習です。

