速さの問題は中学入試では頻出かつ力の差がでる単元です。
中学入試の算数でも速さの問題はよく見られました。
文章題を解く時には頭の中で考えるのでなく、図を書いて条件整理をすることはまずやるべきことです。
この図の書き方ですが、
速さの単元での図の書き方には、
①ダイヤグラム、②状況図(線分図)、③vtグラフ(面積図)
の3種類があることを知っていますか?
速さの単元だと「ダイヤグラム」最強説でどんな問題もダイヤグラムで解いた方がいいと指導する先生もいるようですが本当でしょうか?
日能研では4年生の時からダイヤグラムでの解き方を教えて、状況図は教えないそうですね。
四谷大塚の予習シリーズではまず状況図(線分図)で教わります。
速さの単元の3つの図の書き方を比べてみて、「ダイヤグラム」最強説を検証してみます。
速さの単元の3つの図の書き方
速さの単元での図の書き方には、
①ダイヤグラム
②状況図(線分図)
③vtグラフ(面積図)
の3種類があることを知っていますか?
一般的には、塾では②の状況図をまず習い、ある時に①ダイヤグラムを習って、
これは使える!と「状況図派」と「ダイヤグラム派」に分かれるようです
私個人の見解では、
どれでも自分の得意な図の書き方に持ち込めばいいと思います。
得意な自分のエリアに持ち込むのも大事な戦略です。
2023年洗足学園の問4を使って3つを比較してみる
【問題】
AさんとBさんは山を越えてとなり町まで歩きます。AさんはX町を出発し頂上で30分の休憩をとってY町へ、BさんはAさんが出発した1時間後にY町を出発し、頂上で30分の休憩をとってX町へ行き、BさんはAさんがY町へ着く前にX町に着きました。AさんとBさんは、上り道でも下り道でもそれぞれ一定の速さで歩き、上り道では下り道の3/4倍の速さで歩きます。下のグラフは、Aさんが出発してからの時間とAさんとBさんの間の道のりを表しています。このとき、次の問に答えなさい。
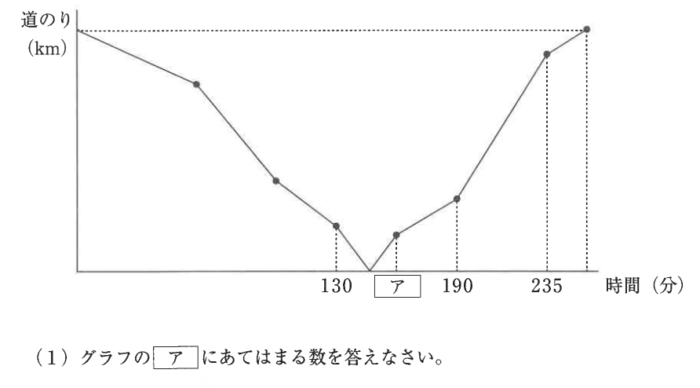
①ダイヤグラム
問題文に2人の距離の差が書かれた図があるので、それを利用してダイヤグラムを作成していきます。
実際に書いてみると分かりますが、ダイヤグラムは時間と場所のポイントを押さえてある程度正確に書けないと問題を解く時に解けなくなってしまいます。
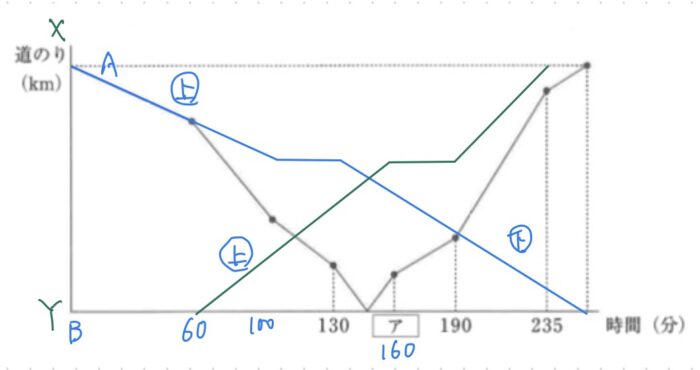
【メリット】
1.それぞれの動きに関する時間と距離の関係が視覚的にわかる。(2次元の情報)
2.相似を使って図形的に解くことができる。
この問題ではデメリットは感じられないが、
【デメリット】
1.問題によってはどこですれ違うのかや、距離感など状況を正しく書けないと
解けなくなってしまうこともある。
正しく図を書けることが前提条件となる。
2.往復が何回もあるようなケースでは図を書くのに困るケースが多い。
そうすると(2)(3)は以下のように解けます。
(2)AさんとBさんの上り道を歩く速さの比を、最も簡単な整数
の比で答えなさい。
X~頂上間は(時間)A:B=100:45=20:9 *Bは下り
Bの登りは9×4/3=12かかるのでA:Bの時間の比はA:B=20:12=5:3
速さの比は逆比になるので3:5
答え3:5
(3)AさんとBさんがすれ違った場所をZ地点とするとき、X町からZ地点とY町からZ地点の道のりの比を、最も簡単な整数の比で答えなさい。なお、この問題は解答までの考え方を表す式や文章・図を書きなさい。
速さの比(A上):(B上)=3:5、(B上):(B下)=5:5×4/3=15:20より、
速さの比(A上):(A下):(B上):(B下)=9:12:15:20
XY間を〇15×100+〇20×45=〇2400とする
〇2400ー〇9×100ー〇15×70=〇450・・・130分後の距離の差
12:15=4:5より〇450×5/9=〇250
ZY間は〇15×70+〇250=〇1300
XZ間は〇2400ー〇1300=〇1100
よってXZ:YZ=1100:1300=11:13
答え11:13
②状況図(線分図)
山登りなので上下を意識するべく線分図を少し変形させています。
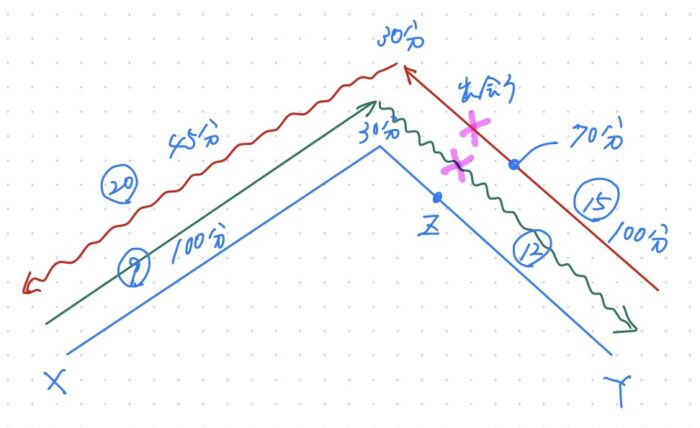
(メリット)
1.図を書きやすい。(正確な条件がなくてもだいたいで条件整理ができる)
2.同じ距離の中での比較をするという原則的なアプローチをしやすい。
3.往復が何度もあるケースでも対応しやすい。
(デメリット)
1.視覚的には距離の感覚がわかるが、時間や速さの条件は文字情報なので1次元の情報になってしまう。
状況図を書く段階で、わかることをどんどん書き入れていくと速さの比などがすぐに決まって書き入れることができました。
これで(2)まで解けています。
あとは出会う地点までの距離を出すだけですが、ここまでわかっていればあとはダイヤグラムで解くのと同じ方法で答えが出ます。
vtグラフ(面積図)
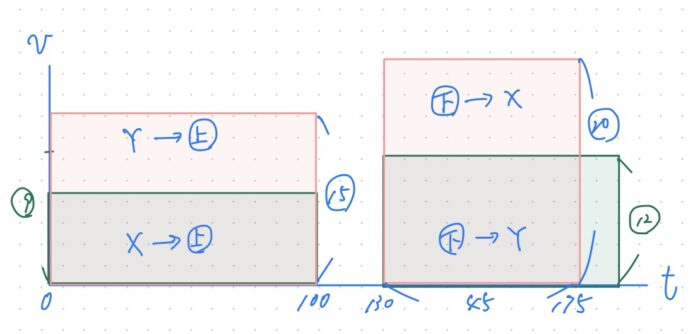
「vtグラフ」ってなじみのない方は多いと思いますが、物理で使うグラフです。
要は「面積図」です。
速さ=距離÷時間
と公式のごとく覚えますが、距離=速さ×時間 を面積図で表しているのです。
緑色の面積の和とピンク色の面積の和は等しいし、クロスの四角形の面積は同じ距離なので面積が等しくないといけません。となると、他の単元でよく使う面積図の考え方を使うだけです。
【メリット】
1.速さと時間という2次元情報を扱うので、面積比較など図形的に処理しやすくなる。
【デメリット】
1.同じ方向に動くのであればいいが、向かい合うなど方向が違うと状況理解が図だけでは難しい。
2.往復のあるケースでは対応が難しい。
面積が同じであれば時間から速さの比を出すことができたりするので、図が描けたら(2)までは同様に解けます。
(3)も同様です。
まとめ
どの図の書き方にもメリットがあればデメリットもあります。
それを理解したうえで問題によって図を使いこなせる力こそが最強説だと思います。
「基礎の勉強」って実は「問題を解く」ことよりも、条件を整理して状況に応じてわかりやすい図を書くことなんです。
それでも好きな〇〇派にこだわりますか?
問題ごとに使いこなせるようになると、考え方の基本はどの図でも同じことを使います。
違うのは状況整理のための図の書きやすさだけです。
問題ごとに使う図を使い分けられるようになると見える世界が変わると思います
ちなみに、中学数学、高校数学に入れば座標というダイヤグラムの進化系で直線の方程式を使って解くという新たな技やベクトル、積分を使って解いたりする方法も使えるようになります。
本来の先取り学習とは、
使える技を増やして、同じ問題を解くバリエーションを増やす
ということなのです。

