
このtwitterのコメント、ものすごく深いですね。
ではこれを身近に体験してみませんか?
東海中学の問7(2)
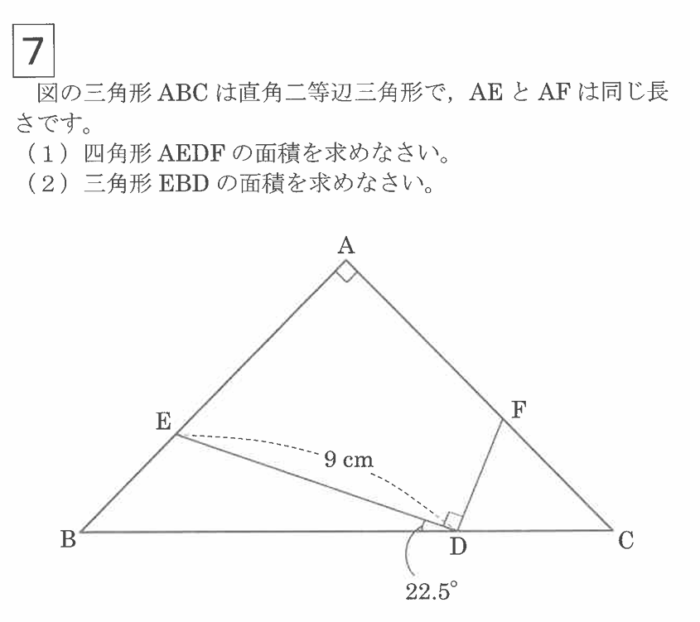

毎年図形問題でなかなか面白くて難しい問題を出題する東海中学です。今年の東海中学の問7(2)は2013年の算数オリンピックファイナルの5番(ファイナリストの正答率33.7%)の左右の向きを変えた数値替え問題でした。
算数星人さんは折り返して、等積変形を利用して解いています。
コベツバさんでは、正八角形を利用して同じく等積変形を利用して解いています。
算数の瞬殺技
この問題は、このような補助線を引くことで合同な三角形を作り出せたら瞬殺でした。7×3.5×1/2=12.25なので東海中学の問題も同様に考えたら9×4.5÷2=20.25と実は瞬殺問題でした。
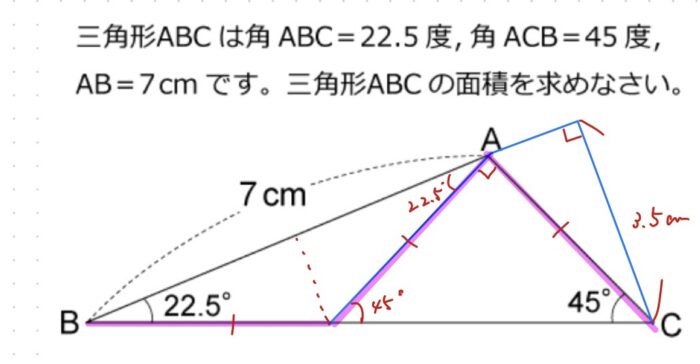
数学(中学生・高校生)で解くとしたら

では最初に中学生が三平方の定理を使って解くとしたらどう解くか?
ちなみの三角形の面積の求め方ってたくさんあること知ってますか?算数なら「底辺×高さ÷2」ですが、高校生になったら全部使いこなせるようにしたいですね。
中学生の解き方
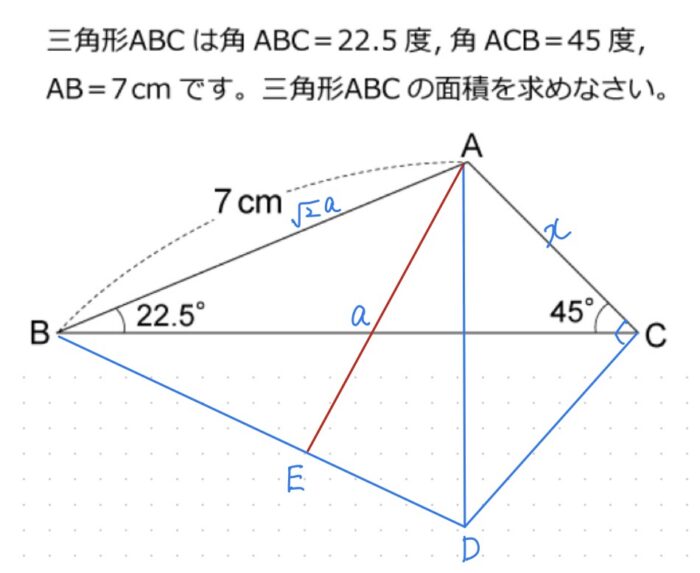
ACをxとします。また、計算の都合上AE=aとします。
すると求める面積Sは△AED+△ADCです。
△ADCは直角二等辺三角形、△ABDは底辺√2aで高さaの三角形です。
そうすると求める面積S=1/2(√2a×a×1/2+1/2×x^2)となり
△AEDに三平方の定理を当てはめればa^2+(√2aーa)^2=2x^2
この2つの式を使って整理すると
S=a^2/2となり7=√2aよりS=49/4=12.25
*ABをaと置かないであえてAEをaにしたところが計算を簡単にするポイントでした。こういう工夫も算数で十分やっています。
高校生の解き方
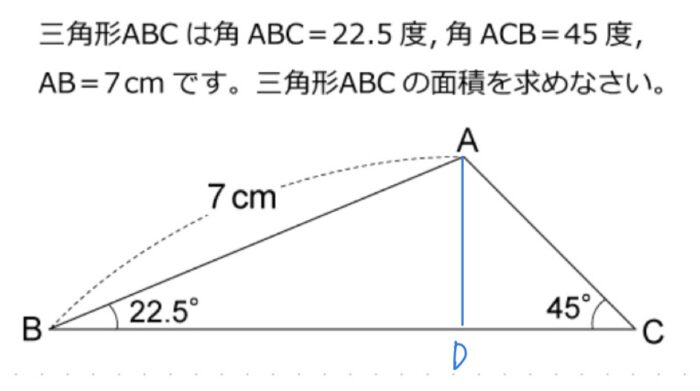
これを知っている人は少ないかと思いますが(教科書や参考書には載っていないので)、
面積公式
S=a^2*sinBsinC/(2sin(B+C))
を使います。
S=7^2×sin(22.5°)sin(112.5°)/2sin(135°)
半角の公式や加法定理を使って
sin^2(22.5°)=(2-√2)/4
sin^2(112.5°)=(2+√2)/4
sin(135°)=sin(45度+90度)=1/√2
これを代入してS=49/4=12.25
この公式はどうやって出すの?
ちなみに上の面積公式の証明としては
点Aから辺BCまでの高さをhとすれば、
h*(cosB/sinB+cosC/sinC)=aが成り立っています。
h=a/(cosB/sinB+cosC/sinC)
=a*sinBsinC/(cosBsinC+sinBcosC)
=a*sinBsinC/sin(B+C)
S=ah/2
=a^2*sinBsinC/(2sin(B+C))
最後に

どうですか?
小学生の算数、中学生、高校生の数学を使って1つの問題をいろんなアプローチで解いてみました。
結局、算数の解き方が一番きれいですよね。
数学になると機械的に解いているように感じませんか?
これが算数での解き方のスマートさ奥深さに魅了される理由です。

