
勉強に関わらずなのですが、何かをする時に必要なことは?
と聞かれたらなんと答えますか。

私だったら「再現性」と答えますね。
では、算数の問題を使って「再現性」ってどういうことを考えてみましょう。
算数の問題
よくある典型問題です。
正三角形のなかにある点を取って、それぞれ垂線をおろすと1cm、2cm、3cmになっています。この時正三角形の高さを求める問題です。
【中学受験算数】理数館の算数の人より
動画では条件を活用して3つの正三角形を作り、平行移動させて高さを求めています。
正三角形はどの方向から見ても同じ形であることをうまく使っていますね。これも「正三角形」という形の性質を利用した再現性のある考え方です。

「再現性のある考え方」とは
どんなふうに問われ方が変わっても「普遍的な考え方」のことを言います。
正三角形の定義と性質
ここで、正三角形の定義と性質をおさらいしておきましょう。

中学生になったら定義と性質の区別はつけられるようにしておきましょう。
定義とはそのものの意味をはっきりと表す言葉です。
正三角形の定義は、3つの辺が全て等しい三角形。
性質というのは、その言葉が持っている特徴のことです。
正三角形の性質は、3つの内角は等しい。
全ての内角が等しいという事は60度ですね。
これらを前提として、正三角形におけるいろいろな特徴を習います。
30°、60°、90°の三角形も現れますね。
算数の瞬殺技
ところで、もちろん動画での解き方でも十分早いのですが、この問題はあることを応用すれば実はほぼ瞬殺で答えが分かります。
計算式は(1+2+3)÷3×3=6cm

これでなんで答えが出るの?
正三角形はどの3辺も同じですね。
ということは問題の図から正三角形の1辺を□としたら、正三角形の面積は□×(1+2+3)÷2で表せます。
ここで正三角形の中にとった点がどこにあろうと上記の式で面積を求めることができることはわかりますね。
であれば、わかりやすく下の図のように正三角形の頂点から下した垂線上に点を取っても同じですね。各辺までの距離は2cmです。(たまたま問題の図から左へ平行移動した点でした。)
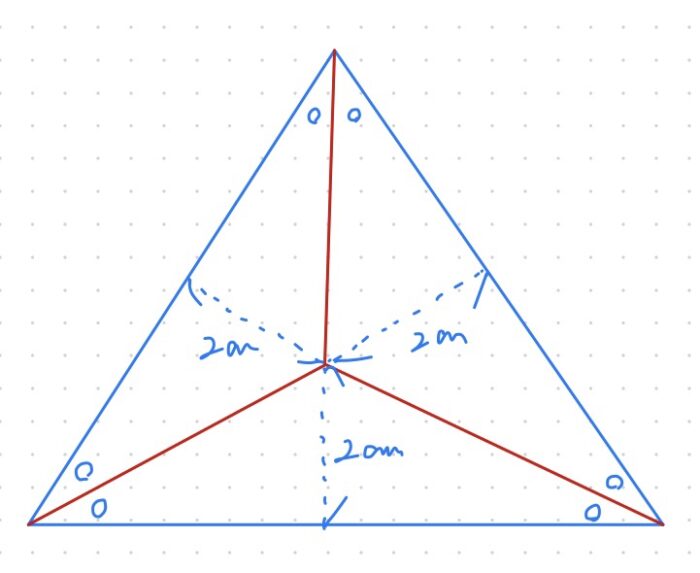
□×(1+2+3)÷2=□×(2+2+2)÷2
そうすると図のように合同な三角形しかも30°、60°、90°の三角形が現れました。なので赤い線は4cmとわかり2+4=6cmとなります。
じつはこの点は正三角形の重心なんですね。
重心は垂線を2:1に分けることから、2cm×3=6cmと求めたのでした。
2023膳所高校入試問題
少し見方を変えた問題ではありますが、答えを出すだけなら頂点から下した垂線の長さと同じになるので6÷2×√3=3√3と出せますね。
さいごに
長さを求める時に、面積を使って求めるアプローチを習いますよね。
その考え方と正三角形の特徴を使いました。
問題を解く時には、何かと何かをくらべるということをします。
線分図をイメージしてもらうと分かりやすいです。
くらべるためには、まずそろえてからくらべます。
かんたんにそろわなければ、ひろげて(拡大、縮小)からくらべます。
今回は面積をそろえてからくらべています。
この基本的な考え方が再現性のある考え方になります。

