
今年の東大文系数学の問題の中に算数で解ける問題がありました。中学生の数学でも解けます。
2023 東大文系数学 問題 pic.twitter.com/ro4W5xiWex
— Natto@人生の攻略本 (@nextonkinlaw) February 25, 2023
この問題を少し表現を変えてみることで、小学生、中学生、高校生の3通りの解き方ができます。
高校生はもちろん三角関数を使いますが、中学生は三平方の定理を使えば解けます。
では小学生はどうやって解けばいいのでしょうか?
問4(1)の問題
【問題】
半径1の球面上の相違なる4点、A,B,C,Dが
AB=1,AC=BC,AD=BD,cos角ACB=cos角ADB=4/5
を満たしているとする。
(1)三角形ABCDの面積を求めよ。
算数用に問題を少し変えてみると
三角形ABCはAB=1,AC=BCです。
Aから垂線を下してBCとの交点をDとするとAC:DC=5:4となる。
(1)三角形ABCDの面積を求めよ。

三角関数は高校数学で出てくるのでそこを変えてみました。
高校生、中学生、小学生の3通りの解き方
小学生の解き方
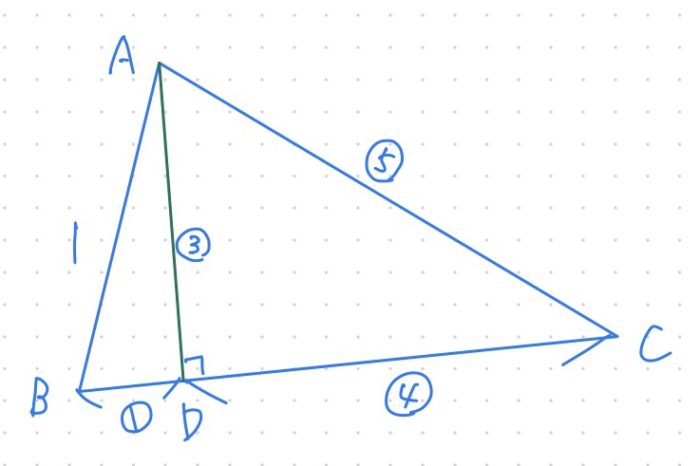
△ADCは3:4:5の直角三角形とわかる。
△ABDにおいてBD:AD=1:3。
CからABへ垂線を下した足をEとする。EはABを2等分するのでBE=1/2
△ABDと△CBEは相似となりBE:CE=1:3よりCE=1/2×3=3/2
△ABC=1×3/2×1/2=3/4

3:4:5の直角三角形と相似を利用して解くことができました。
中学生の解き方
中学生の場合は
△ABDにおいてBD:AD=1:3からBD=aとしたらAD=3a
a^2+(3a)^2=1よりa^2=1/10
△ABC=5a × 3a ×1/2=15/2*a^2=15/2×1/10=3/4
高校生の解き方
AC=BC=aとおくと余弦定理より
1=a^2+a^2-2a^2*cos角ACB
∴a^2=5/2
cos角ACB=4/5よりsin角ACB=3/5
△ABC=1/2×AC×BC×sin角ACB=1/2×5/2×3/5=3/4
さいごに
元の問題は、三角関数で習う単元の公式に当てはめれば簡単に解ける教科書レベルの問題でした。
今回の問題は、3:4:5の直角三角形が見え、かつ二等辺三角形の性質を使ったので算数で解けました。
sinやcoが表す意味を考えれば、中学生でも解けた問題でした。
条件が意味することを読み解くことで他の解法も見えてくることもあります。

