今回は雙葉中学校です。
雙葉中学校の算数
算数は５０分で大問５つ、小問数で１２問でした。
１問にかけられる時間は４分です。
問題は例年と同様、塾のテキストで習うような典型問題をベースにした標準レベル問題です。塾の模擬試験で出題されるような問題です。
雙葉的王道とも言える傾向、それは“丁寧に堅実に”というもの。
どんなにひらめき・直感・着眼点が鋭くても、作業・処理が大雑把な生徒は高得点が望めない算数です。
問４ 水量の問題
今年度の入試で差がついたと思われる問４。この問題は問題文を「算数語」へどのように変換したらいいかを考えるのにいい問題です。
https://laughwaku.com/shikourilyoku/
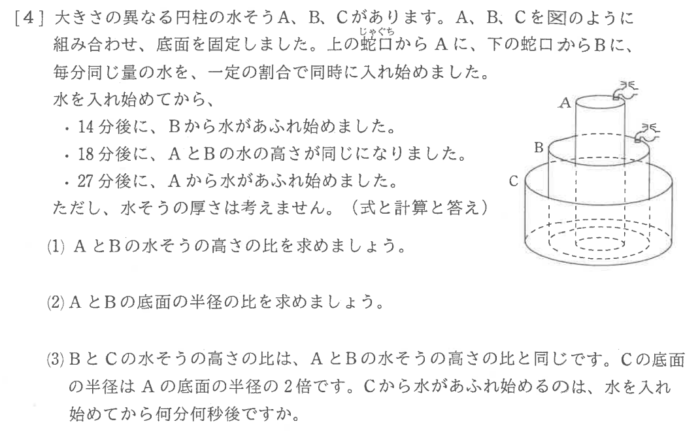
（１）Aの水そうを基準にするとA:B＝27:18＝3:2
答え３：２
比べる基準をそろえないと比べられません。ちょうどAをベースにBの高さを表す条件が書いてあるので、それをBの高さと読み替えます。
A,Bともに同じ水の量を入れていることから、14分後にBからあふれ、その４分後にAの水槽ベースでBの高さまで水が入るから、Bの水槽は18分でいっぱいになる。だからA:B=27:18＝3:2と出したらたまたま答えは同じですがこれは違いますよね。最初の14分間でAにも水は入れていますよ。（２）の問題に関係します。
（２）Aは27分でいっぱいになる。Bだけでは32分（=14+18）でいっぱいになる。（１）からAとBの底面積の比はA:B=27/3:32/2=9:16
求めるのは半径の比なのでA:B=3:4
答え３：４
水槽の体積は（底面積）×（高さ）もしくは（１分間の量）×（時間）のどちらでも表せることに気づけることがポイントですね。
（３）条件から（高さ）A:B:C＝9:6:4、
（半径）A:B:C=3:4:6だから（底面積）A:B:C=9:16:36
それぞれの水槽の実際の底面積の比はA:B:C=9:7:20
Bは（底面積）7×(高さ）6=42を14分でうめる。
Cは（底面積）20×（高さ）4=80をうめる時間を考える。ここで14分後から蛇口１つ分。さらに13分後の27分経過からは蛇口２つ分であることに注意する。（42を７分でうめることになる）
44をうめるにあたっては蛇口１つで13分、残りを蛇口２つでうめる。
蛇口１つで42×13/14=39、のこりは41。
7×41/42=6と5/6分=6分50秒。27分＋6分50秒＝33分50秒
答え33分50秒後
（３）はていねいに解かないと正しい答えになりません。試験では後回しにする問題だったかもしれませんが、（２）を解く時のポイントを踏まえて考える問題でした。
【中学入試2023】独断と偏見の良問紹介シリーズ
https://ameblo.jp/daigorobe/entry-12787212821.html
Follow me!
