お子さんが算数の問題をよく間違えるのであれば、塾の先生に
女性何を強化したらいいでしょう？
女性どこが弱いでしょう？
と相談したくなりますよね。
どこを間違えるかを考える際に、どういう過程を経ているかを見る必要があります。
ところで、算数の問題を解く時に４つの段階があることを知っていますか？
今回はその「算数の問題を解く時に４つの段階」について紹介しているYoutube動画をもとに、その４つの段階について少し深堀してみます。
そして算数の問題を間違えるメカニズムについて考えてみたいと思います。
算数の問題を解く時の４つの段階
- 第１段階：問題文の読解、何が書いてあるのかを読み取ること
- 第２段階；条件を整理すること
- 第３段階：テクニック、解法を当てはめる
- 第４段階：計算をして答えを出すこと
コテツでは、この４つの段階のうちどこで一番子供が間違える、もしくはひっかかると思いますか？
お子さんは、だいたい決まって
１．テクニック、解き方を知らなかった
２．単純な計算ミスをしてしまった
３．難しいわけではなくて問題の条件を勘違いした、条件を読み落とした
４．全然わからなくて手も足も出なかった
という答えに集約されませんか？
４の「全然わからなかった」は１に近いかもしれませんが、１はなんとか解こうとチャレンジしてみたけど、解けなかった問題です。
３の読み間違えてしまって勘違いしたとか、条件を読み落としたとかって解けなかった原因をそこに求めることは、解けなかった事実を簡単に考えていることになるので実は危険です。
私は、
第１段階の問題文の読解、何が書いてあるのかを読み取ることがそもそもできていないことに主な原因があると思っています。
ではそれはどういうことかを考えていきましょう。
読解力を鍛えるとは？
読解力とは必ずしも文章題に限りません。
計算問題でも、場合の数の問題でも、図形問題でも読解力は必要です。
読解力とは問題の条件を整理して問題の作者の意図を考えることです。
いくつかの問題を通して私が考える読解力とは何かを紹介します。
ちなみに計算問題や文章題の読解力を紹介した問題については、以下の記事で書いています。
場合の数の問題
【問題】
黒石３個と白石７個を一列に並べます。この列が２つ以上の連続した白石の両端に黒石があるという部分を含むのは何通りありますか？
単純な並び方の問題に制約条件をつけることで少し難しくした問題です。
場合の数の問題の場合は、書き出しが基本ですが、この問題で書き出しをやると大変です。
そんな場合は「余事象」を考えればいいと気づけるかどうか。
余事象は習いますからね。
そこで、①黒石３個が並んだ場合、②黒２個と黒１個の組み合わせの場合、③黒石を３か所にばらす場合
で考えると
全部の場合は10C3=120通り。①は８通り、②７×２＝１４、③６通り
１２０－（８＋１４＋６）＝９２通り
ここで、使う考え方は条件を満たさないように「かたまり」を作って組み合わせを考えるということ。
これが読解です。
図形の問題
【問題】
右図のように∠A＝60°、∠B＝90°である直角三角形ABCの辺AB、BC、CA上にそれぞれ点P、Q、Rをとって結んだところ、∠P＝60°、∠R＝90°になりました。このときARとRCの長さの比を最も簡単な整数の比で表しなさい。
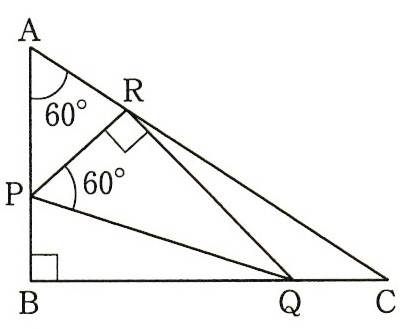
図形の見方を変えたら瞬殺問題です。
図形問題は条件の整理とともに、図形の見方・とらえ方も読解の要素の１つです。
お子さんは算数の図形問題の時にどのように解いていますか？
テキストの図形を使って解いていますか？
それではいつまでたっても図形問題は得意にはなりません。
図形問題は、自分で図を書くこと！
これは小学生に限らず中学生、高校生も同じです。
塾の先生が解説のために黒板に図形を描きますね。
先生の解説は図を書くところから始まっています。
お子さんはどのように先生が図を書いているか意識して見ていますか？
先生はその問題の図形のポイントを意識しながら黒板に書いているはずです。
そして問題の図が正しいとは限りません。
自分で図を書くことで問題の図形の特徴を実感することができるのです。
この問題、条件に当てはまるように自分で図を書いてみてください。
条件を満たすために必要なことが見えたら瞬殺のはずです。
数の性質の問題
【問題】
次の性質を満たす整数を小さい順に３つ答えなさい。
・約数を６個以上持つ
・約数のうち大きい方から６つの和が自身の２倍と一致する
例えば、１００の約数は９つで、約数のうち大きい方から６つの和は
１００＋５０＋２５＋２０＋１０＋５＝２１０
なので、条件を見たしません。
大きい方から6個の和がミソですね。
6年生なら1度は見たことがあるかもしれない数の問題からですが、一見歯ごたえのある問題だと思います。
この問題の裏に隠れたテーマがわかれば3つだけでなく何個でも答えはすぐに出せます・・・。
つまり読解力です。
３つ答えるのですが、１つは知っていればすぐに答えられます。
残り２つはどうやってみつけましょうか？
さいごに
私が見つけた動画はこちらです。
実はこのテーマ、算数が苦手なお子さんだけでなく算数が得意で模試の偏差値もが高いお子さんにも当てはまります。
実は算数の偏差値が高くても目先を変えた見たことのない問題になると解けないのは暗記算数になっていませんか？
