私が常日頃から言っている算数の問題を解く時の大事なステップは「そろえる、(ひろげる)、くらべる」です。
くらべるためにそろえて、くらべることで差を浮きだたせて、その差が何にあたるのかを考える。
どの問題でもこれがフォーマットです。
私が転職した先での若手の部下の口癖が「差分」でした。
新入社員のころから常に「差分」を考えろ!と教育されていたようで、私にとっては新鮮でした。
その会社では物事を
「結果に至るまでの過程を因数分解して、理由となる差分を考えろ」
という哲学でした。
これは算数に限らず「考える」という時の考え方に通じるものです。
お子さんは「差分」を意識しているでしょうか?
今回は日能研のゴホンゲ先生のブログで2023年洗足学園3次試験問題を紹介されていることをヒントに、算数の入試問題を通じて「差分」を考えるとはどういうことかを見ていきます。
2023年洗足学園3次試験問題から
【問題】
たくさんのアメがあります。1 袋に 20 個ずつアメをつめると 18 個あまります。 150 個のアメと 1 つの袋を追加して,1 袋に 24 個ずつアメをつめると,最後の 袋には 4 個足りませんでした。最初にアメは何個ありましたか。
過不足算と言われる単元からの出題です。
日能研のゴホンゲ先生は、
 ゴホンゲ先生
ゴホンゲ先生このレベルの問題を、ごく最初の方に「ここで点数確実にとってよ!」とばかりに突きつけて来る、さすがに今年も東大20名以上合格を出して難関校としての位置づけを確固たるものにしつつある学校だな、と感じます。ただ実際のところ、難関校受験するなら確かにこのレベルは確実にモノに出来ないといけないとも感じます。
マルイチ算で解く
この程度の問題であれば、図を書いたうえでマルイチ算を使ってさらっと解いてしまうお子さんも多いでしょう。
まずこの問題は「2つの状況を比べる」ということがポイントです。
2つの状況を正確に図に落とし込んで比べてみます。
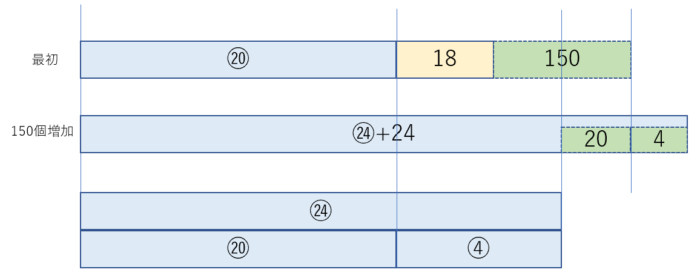

最初の袋の数を〇とすると、
⑳+18+150=㉔+20 と立式出来て、①=37とわかり
アメの元の個数は20×37+18=758個と求められます。
「同じ量のもの同士で比べて解く」というのは方程式的な側面が強いです。
算数ではマルイチ算といいつつ、移項という考え方をあえて使わないようにして方程式を解いているのと同じです。
ただこのマルイチ算で解くことに慣れてしまうと答えは出せますが、本当の算数の力、考える力をつけることができるのだろうかと思うのです。
というのも、等しい関係を見つけることは当然考える力を必要としますが、そのあとは機械的に答えを出せてしまうからです。
算数的な考え方で解く
算数的に考えて解くとは、数字の動きをとらえながら結果の原因となる差分を考えて、その差が何にあたるのかを考えるということです。
どういうことかというと、「自分で袋に詰める身になって考えてごらん」ということです。
つまり、20個ずつ袋に入れて十何個余って詰め直すからと言って、
「それを全部取り出してから」
詰め直したりはしないよね、ってことです。
20個ずつ入れる場合と24個ずつ入れる場合を比べて20→24で1袋に4個ずつ追加して詰めればいいってなります。
この「1つ当たりの差」に注目して、それが積み重なって結局「全体で何個(袋に詰める量が)変化したか」に注目して式を作りなさいってことです。
つまり基本的な過不足算の場合は、「同じ袋の数に詰める場合」を比べますし、なおかつ「途中で個数を増やしたりしないで」それで2つの配り方を比べて解くはずです。
だからそのフォーマットに直して考えると、(24個入れる)袋を1つ増やさなければ、入れる個数は24個少なくて済む(余る分が増える)。
でも、150個追加しなければその分足りなくなるわけですから、もし最初の詰め方と同じ袋の数で同じアメの個数配ろうとしたなら、4不足→20余り→130不足と結果的にはなるわけです。
すると4個ずつ増やして袋に入れると18個余ってたのが、130個不足になるから結局4個ずつ増やして袋に入れると148個詰める量が変化したので、37袋あるとわかって問題が解けるわけです。
(150+18-20)÷(24-20)=148÷4=37
まとめ
算数的に考えて解くとは、数字の動きをとらえながら結果の原因となる差分を考えて、その差が何にあたるのかを考えるということでした。
この数字の動きこそが結果の原因となる「差分」なのです。
算数の問題を解く時には「差分」を意識して問題を解く習慣が大事だと思います。





