算数において図解は重要な技術となります。
4年生、5年生の間は答えを出すことより図を書くこと、式を立てることを最重要として算数を学びましょう、と私は言いたいです。
これが出来る子、出来ない子で12歳以降の伸びは全く変わってきます。
一度、通われている塾の講義を見学してみるとわかりますが、先生が「この問題はこの図を書くんだよ!」と説明します。
先日upしたブログ(「速さの問題でダイヤグラム最強説って本当?ダイヤグラム派、状況図派?」)でも私は速さの問題を解く方法として3つの図を紹介しています。
でも重要なのは
「なぜ、(先生はorそのテキストでは)その図を書くの?」
って疑問に思うことです。
その「なぜ?」について紹介します。
数の2つの概念とわり算の2つの概念
「順序数」と「集合数」
図の種類の前に、小学1年生で習ったことですが、「数」には「順序数」と「集合数」という2つの概念があることを知っていますか?
「前から3人目の人は立ってください」は、前から3番目にいる1人だけをさします。
このときの「3」は「順序数」です。
それに対して、「前から3人立ってください」の「3」が「集合数」です。
つまり、「third」と「three」の違いです。
「等分除」と「包含除」
またわり算には「等分除」と「包含除」という考え方があることも知っていますか?
全体をいくつかに同じように分けることを等分除と言います。
等しく分けきるというイメージで,全体量に対し1あたりの量を求めるという意味です。
全体をいくつかずつに分けていくことを包含除と言います。
全体量を分けていったとき,いくつ分になるかを表す意味です。
- 等分除:「1つ分の数」=「積(掛け算の答え)」÷「いくつ分」
- 包含除:「いくつ分」=「積」÷「1つ分の数」
1.線分図
長さで量を表し、和や差を見るのに使用します。長さの和や差がそのまま見えます。
【問題例】
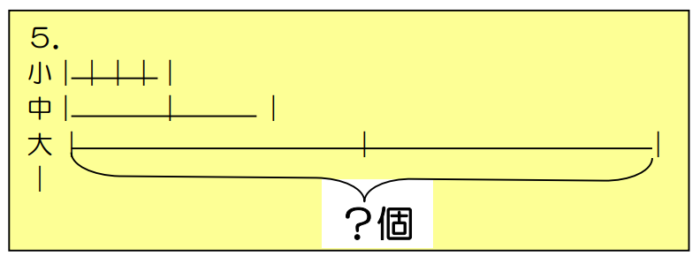
大きさのちがう3種類の箱があります。
小の箱にはケーキが4個入ります。
中の箱には小の2倍、大の箱には中の3倍入ります。
大の箱にはケーキが何個入るでしょう。
2.数直線
長さで量を表し、ポイントで順序を表します。物の大きさや数の和などを見るのに使用します。
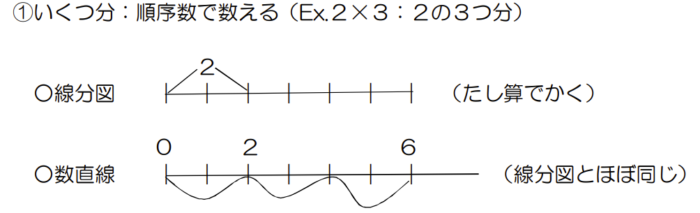
①位置と順序、そして長さで量を表す。(線分図とほぼ同じ。):たし算とひき算を表す。
②位置と順序だけを表す。:かけ算とわり算を表す。
(1)かけ算の場合
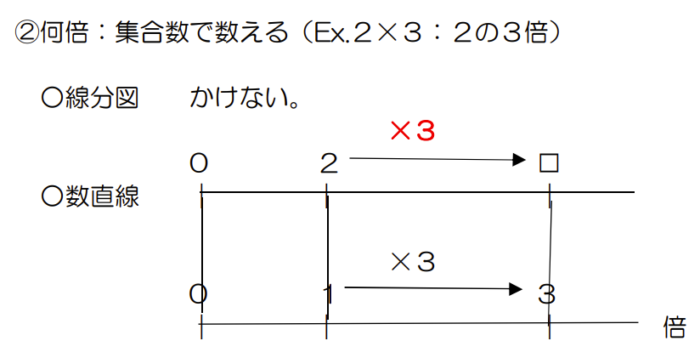
(2)わり算の場合
「等分除」と「包含除」で書いた図の意味が変わります。
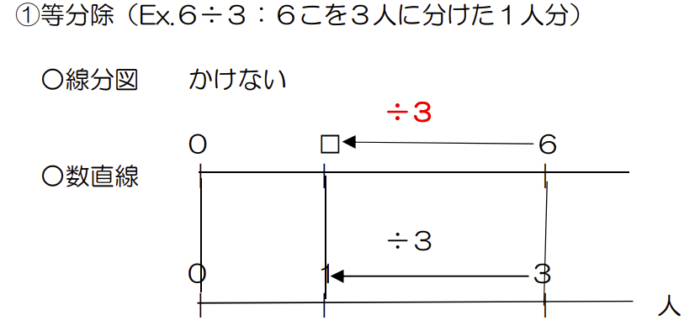
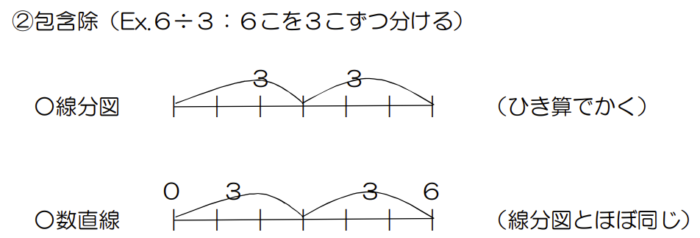
数直線の「0」は、順序数の「0」というより、起点を表す「0」と考えたほうがよい。
3.面積図
2数の積を表現します。長方形の面積公式ですね。
文章で書かれている内容を長方形の面積に置き換えた図です。
たてには「1あたりの量」、横には「個数」「人数」「回数」などをとり、面積は、総数や合計を表します。
【問題例】
1冊90円のノートを15冊買うといくらになりますか。
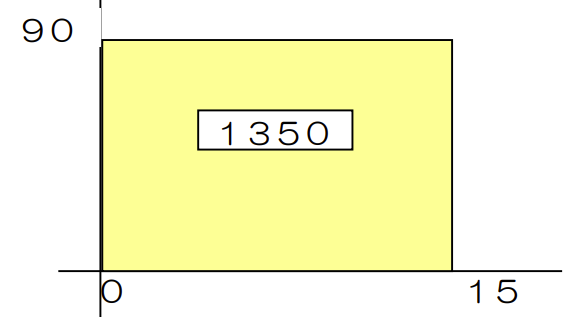
面積図を使う例
| たて | よこ | 面積 | |
| 速さの問題 | 速さ | 時間 | 進んだ距離 |
| 平均の問題 | 平均 | 人数(回数) | 総合計 |
| 仕事の問題 | 1時間あたりの仕事量 | かかった時間 | 仕事量 |
4.グラフ
2量関係を表すのに使います。
小学生で習う比例、反比例は非常に重要です。
「速さ」の単元で用いるダイヤグラムがまさにそうです。
横軸で「時間」、縦軸で「距離」を取ることで時間と位置の関係を視覚化します。
親子で学ぶIINA算数教室
今回、算数で使う図の種類と図の意味について書こうと思ったのは、大阪で親子で学ぶIINA算数教室を運営されている榎本先生のブログがきっかけでした。
榎本先生とは息子の受験の伴走をしている時に知り合って以来、息子は時間の都合上、塾生ではありませんでしたが今でも懇意にさせていただいております。
