数学の網羅系参考書で有名なのは「チャート式」「フォーカスゴールド」「レジェンド」が有名ですね。
これらは典型問題を解けるようになるための指南書であり、学校ではだいたいこの3つのうちのどれかが推奨されているはずです。
今回は、教科書では曖昧なままになっている「論理」の勉強に正面から向かいあっていて網羅系の参考書と一線を画した東進ハイスクールの人気講座「数学の真髄」を担当されている青木先生が執筆された「数学の真髄」を紹介します。
青木先生はかつてSEGで教えていたこともあり、SEGの高校1年生の内容を一部まとめた内容だそうです。
私は息子の中学受験の伴走が終わり、30年ぶりにもう一度高校数学を取り組みなおした際に後に紹介する「論理学で学ぶ数学」に出会い、世界観が変わりました。
絶対必要な参考書かと言われればそうでないかもしれません。
逆に言えば「論理」の勉強をすることで今まで見てきた「受験」数学への世界観が変わるはずです。
高校数学の目的
高校数学の一番の目的は、社会に出てからどうしても必要になる「論理的思考力」を鍛えることです。
算数で習った「たしざん、ひきざん、かけざん、わりざん」は「数学の道具」であり、それらを応用したものがsinやcos、微分積分にすぎません。
みなさんは「たしざん、ひきざん、かけざん、わりざん」の意味をきちんと説明でき、それらを使ってsinやcos、微分積分の考え方を説明できますか?
論理はこの道具を使って、解答を導き出すためのつなぎの役割(思考法)と言えます。
入試問題が解けるようになるためのポイント3つ
入試問題が解けるようになるための3つのポイントをあげるとしたら、
- 確かな数学的知識
- 典型問題を首尾よく解けるようになるまでの経験
- 柔軟で自然な発想力
①と②をベースとした③の発想力を問うているのが難関校の入試問題です。
①②は網羅系参考書でしっかり勉強したら習得はしやすいですが、独学で③を習得するにはなかなか難しいものがあります。
③を習得するとっかかりとして「数学の真髄」は最適だと思います。
「数学の真髄」の紹介
- 本書の目標
- 論理の本質的な理解
- 実践演習を始める前の論理的思考力の養成
本書の特徴は以下の4点になります。
1.論理の基本が身につく「講義」
教科書では曖昧なままになっている「論理」に正面から向き合い、「定義に従って数学を構築する」ことの基礎を学んでもらいます。さらに論理記号を積極的に使い、できる限り曖昧さのない論証ができるようになることを目指しました。
「命題」とは何か。「条件」とは何か。数学の理解はすべてここから始まります。そして「かつ」と「または」を理解し、それがやがて「全称」と「存在」の概念に発展する。ここを疎かにすると、正面から数学と向き合うことができなくなる。易しくはないがこれが基本です。
2.「解き方」ではなく「考え方」を伝授
数学の問題は、レベルが上がるほど「考えて解く」ことを必要とします。どうしたら初見の難問を意味を変えずに易しい問題に帰着させられるのか、その考え方をできる限り詳しく解説します。
数学の問題のほとんどは「ややこしいものを意味を変えずに簡略化する」というゲームだ。だから初心者は「簡略化」の方法を学ぶ必要がある。その基本が「同値変形」です。
東大では頻出の領域問題を解く時の発想法、「順像法」「逆像法」についても同値変形を使って解説されています。
3.「公式を自作して使える」ように指導
「公式は暗記して使うもの」ではなく、「公式は意味を考えれば当たり前、いつだって作れるぜ」というのが賢い人の感覚です。その考え方を実際の入試問題にどのように適用できるのかを伝授します。
4.論理的な答案作成力を鍛える「実践問題」
「講義」で学んだ考え方をすぐに応用できるよう、各Partの最後に実践問題を収録しました。
大学入試問題などの演習を通して、論理的な答案を作成する力を鍛えることができます。
放物線と相似
みなさんは、すべての放物線は相似であることを説明できますか?
放物線では難しいので、半円を扱った「2023年浦和明の星女子中学」の入試問題を紹介します。
【中学入試2023 浦和明の星女子】問1(6)と楕円の面積を求めてみよう!
【問題】問1(6)
右の図のように半径2cm、3cm、4cmの半円と直線を組み合わせてできた図形があります。斜線部分の面積の和を求めなさい。ただし円周率は3.14とします。
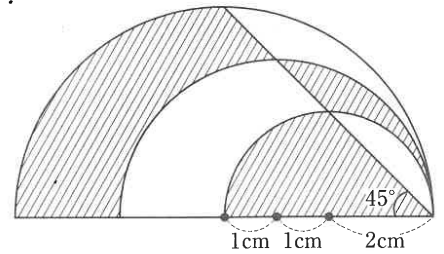
半円を左方向に引っ張って伸ばした図形を重ね合わせています。
3つの図形が相似の関係にあると理解できれば解ける問題でした。
放物線の場合はどうでしょうか?
座標平面上の放物線は、適当に回転し、適当に平行移動することでY=aX^2の形で表せます。
これがY=X^2と相似であることを示せたらいいのです。
Y=aX^2上のどの点も1/a倍したらY=X^2上の点に移ります。
つまり
相似とは「一つの図形を一様に拡大または縮小すると,他の図形と完全に重ね合わせることができること」
でしたから1/a倍すると完全に重ね合わせることができるので相似の関係にあると言えるのです。
数学的に説明するとしたらもう少し式の変形による展開が必要ですが、説明の流れとしては上記になります。
なかなかこういうことは網羅系の参考書では勉強しないですよね。
そもそも相似は中学受験や中学数学で習ったことですが、それが放物線にもあてははまるなんて説明してくれる先生がどれだけいるのでしょうか?
その他の論理関連の参考書
「数学の真髄」と同様に論理を学ぶ参考書として2つ紹介します。
私の主観で3冊の取り組みやすさ、難易度を表示しました。
まずはどれか1冊をマスターすれば他の2冊も取り組みやすくなると思います。
| 数学の真髄 | |
| 問題文の読み取り方 | |
| 論理学で学ぶ数学 |
総合的研究:問題文の読み取り方
数学の問題を解く際に必要な「数学の読み取り方」を学んで、副次的に「問題文を読み取れる」ようになるというのが目的の参考書です。
その読み取り方を学ぶために「論理」の理解が必要不可欠であるため、全編にわたって論理の勉強ができます。
総合的研究:論理学で学ぶ数学
私が最初に出会った「論理」の参考書です。
高校数学や大学入試問題を素材として、数理論理学の記号と方法を数学自身の理解の深化を目指して実践的に説明した参考書です。
まとめ
今回紹介した3冊の参考書はなかなか網羅系参考書ではしっかり勉強できない「論理」をメインテーマに扱っています。
3冊すべておすすめの参考書です。
青木先生は、数学の問題のほとんどは「ややこしいものを意味を変えずに簡略化する」というゲームだ、とおっしゃっていますが、社会に出てからも複雑なものを本質をとらえて簡略化していく力が問われることを実感しています。
その力を鍛えるために「論理」の勉強を時間をとることは後々役立つと思います。
(追記)
数学の真髄の「ベクトル編」も発売になっています。









