今年の一橋大学の数学の問題はデータサイエンス学部ができるからなのかわかりませんが難化したそうです。
問4の規則性の問題の(2)は(1)を前提としたならば算数でも解ける問題です。
ぜひ考えてみてください。
問4群数列の問題
Twitterで知りました。
問4の問題は、算数でもみかける群数列の問題です。
ななめに右下から左上に向かって数字が増えていく規則性です。
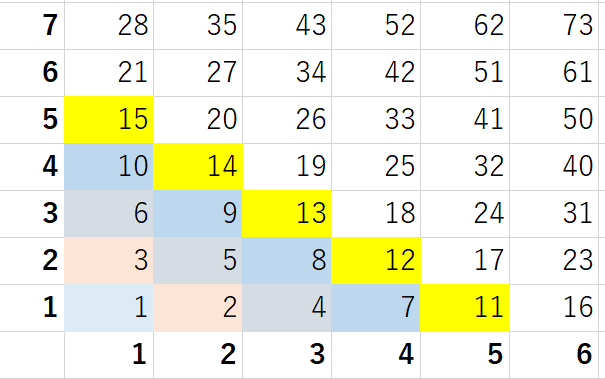
(1)はたとえば9+19=2×14となることを証明する問題です。
(2)は四角形で囲める4つの合計が2023となる場所を求める問題です。
算数なら、(1)の規則性を示して、それをつかって4つの数を答える問題にできるでしょう。
数学で解くなら
(1)
たとえばf(2,4)=14はななめの5列目に入っています。
なので2+4-1=5列目といえるので、(m+n-1)列。
(1~5)までの和から(m-1)を引くと15-(2-1)=14と言えます。
これを一般項で表せば1/2×(m+n-1)(m+n)-m+1となります。
同様に一般項で表して、左辺と右辺が同じになることを示せばいいです。
(2)
右辺が(m+n)(m+n+1)-2m+2と表せることを使うと
上の式をAとおいたら2×Aー1=2023を解けばいい。
式を展開すると(m+n)^2ー(m-n)=1010
これを満たすのは(m,n)=(23,9)
ちなみに一般項1/2×(m+n-1)(m+n)-m+1に代入すると
(m,n)=(23,9)=474です。これは左下の数字です。
算数で解くなら
(1)の規則性を使って、左上数を□とします。
4×□ー1=2023より□=506とわかります。
この506がどの列に入っているかを考えます。
31列の一番左は496、32列の一番左が528だから32列に入っていることがわかります。
528からスタートして506はf(23,10)とわかります。
f(23,9)は496からスタートして474。f(24,9)=505。
f(24,10)は33列が561からスタートするので538。
つまり474,505,506,538の4つの数とわかりました。
